Tag Archives: Interval

Lesson 12: 6th and 7th Chords

Remember you can zoom in and out on the images in this post by pressing Ctrl + and –

In a previous lesson about chord progressions you may have noticed chords with a 7 behind them V7 or IIm7, examples of which are the G7 and Bm7 chords. These are called 7th chords.

7th chords are chords that consist of 4 notes, starting with a Major or minor triad and playing an extra note on top.

Before I show you how to construct and play these chords let me briefly touch on the naming of intervals and chords. The names 7th and 6th refer to intervals used in these chords. So far in these lessons I’ve avoided using the standard interval names, such as minor 2nd and Perfect 5th because in my opinion they only confuse guitar players who are just starting to learn music theory. The number one priority at this stage is to know how to construct chords and scales and to be able to see them easily on the fretboard.

In future lessons I’ll talk more about standard naming conventions for intervals and then you’ll be able to discuss Augmented 9ths and Perfect 11ths with piano and violin players as much as you want.

Using our method of counting the fret distance from the root note you should easily be able to remember the formulas and apply them to the fretboard using the Five Fret Pattern. Remember the formula for the Major triad is 0 – 4 – 7 and for the minor triad it’s 0 – 3 – 7.

Below you’ll find the name of the chord, the common symbol for it, the formula, an image of all the notes for that chord across the fretboard and an example of of a voicing of that chord. Note that the chord shapes shown are moveable along the fretboard, just play the same shape at different places along the fretboard.

Name: Major 7th
Symbol: M7 of Maj7
Formula: 0 – 4 – 7 – 11
Example: BbMaj7: Bb, A, D, F

Bb Major 7th Notes

Example Voicing: BbMaj7

Bb Major 7th

Name: Dominant 7th
Symbol: 7
Formula: 0 – 4 – 7 – 10
Example: Bb7: Bb, G#, D, F

Bb Dominant 7th Notes

Example Voicing: Bb7

Bb Major Dominant 7th

Name: Major 6th
Symbol: 6
Formula: 0 – 4 – 7 – 9
Example: E6: E, G#, C#, B

E Major 6th Notes

Example Voicing: E6

F# Major 6th

Name: minor 7th
Symbol: m7
Formula: 0 – 3 – 7 – 10
Example: Bbm7: Bb, C#, F, G#

F minor 7th Notes

Example Voicing: Bbm7

Bb minor 7

Name: minor 6th
Symbol: m6
Formula: 0 – 3 – 7 – 9
Example: Bm6: B, D, F#, G#

B minor 6th Notes

Example Voicing: Bm6

B minor 6

Learn the formulas for each of these chords and see how many different ways you can play them along the neck, there are quite a few positions for each chord.

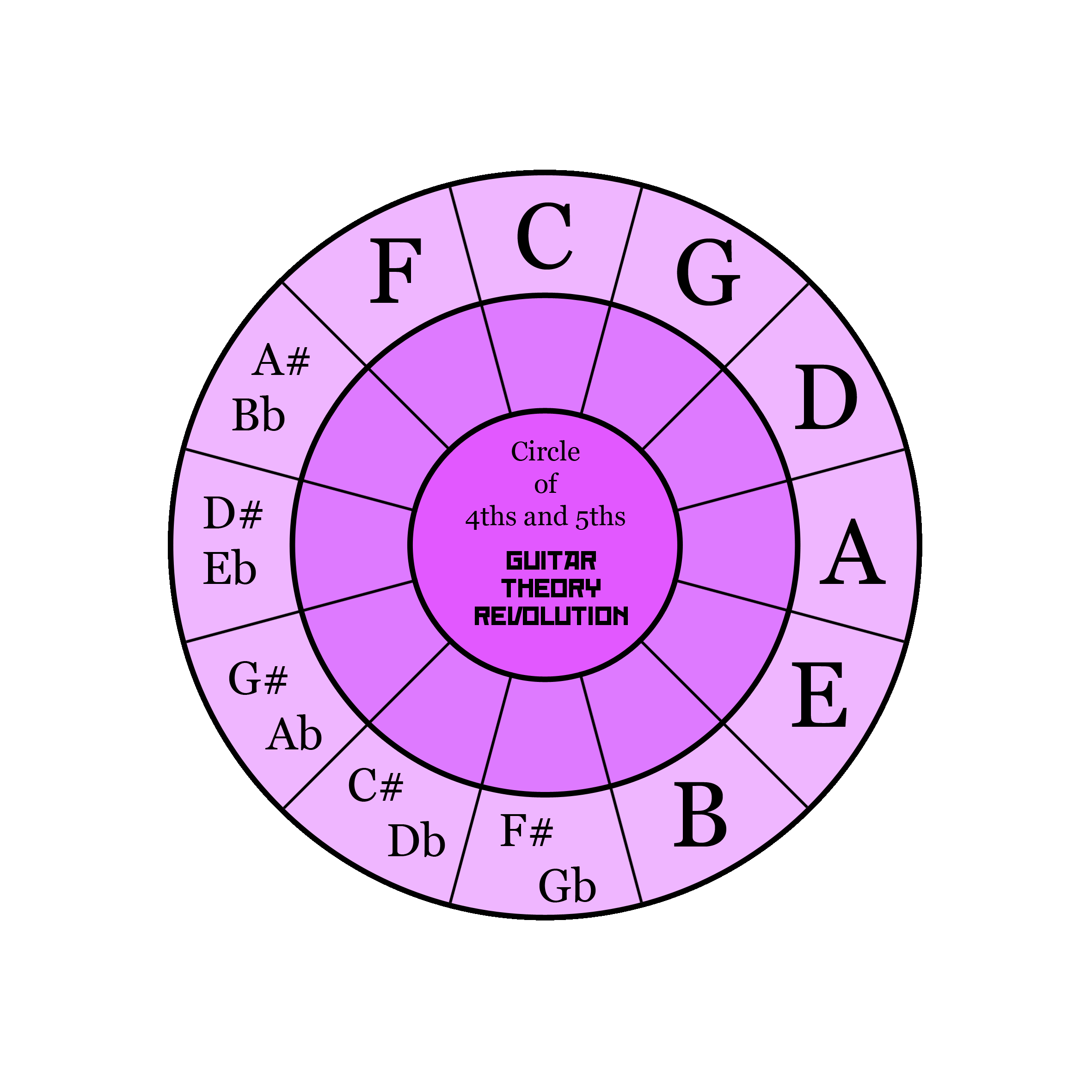
Lesson 9: The Circle of 4ths and 5ths

Circle Of 4ths and 5ths

The circle of 4ths and 5ths is a way of visually representing the relationships between the 12 tones of the chromatic scale. It is one of the most useful tools you can use to understand music theory because it gives you insights into the fundamental way that Western music works.

The great thing is that standard guitar tuning follows the circle of 4ths and 5ths so if you’ve followed previous lessons (Lesson 6: The Five Fret Pattern and Lesson 8: The BEAD-GCF Pattern) you’ll already know a lot about the circle. This lesson will show you how to find the notes in the circle as well as some practical applications for your guitar playing.

The order of the notes around the circle (which determines their relationship to each other) can be found as follows. Starting at the top with C (though you an start with any note) you can find the next note in the clockwise direction by finding the next note 7 notes along in the chromatic scale (the chromatic scale is all 12 notes) as follows: C – C# – D – D# – E – F – F# – G. The interval name of this 7 note / fret distance is the Perfect 5th.

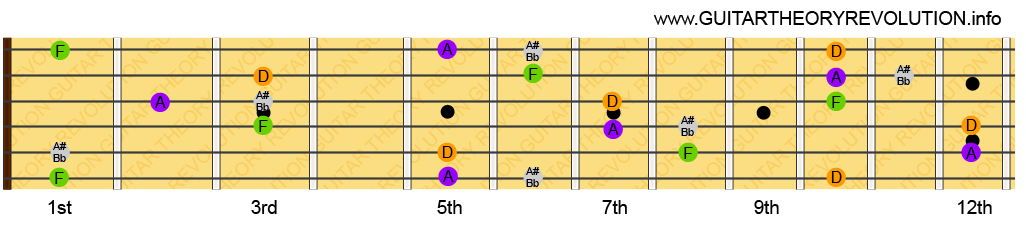
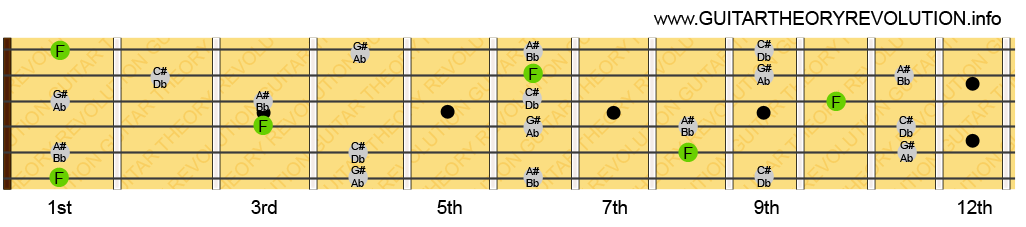
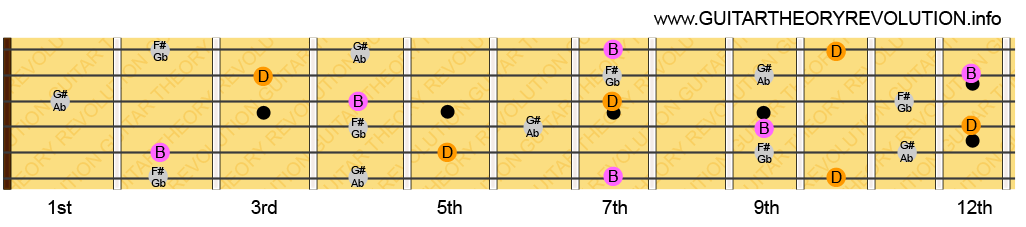
To find the next note name in the clockwise direction we move another 7 notes up the chromatic scale (or 7 frets up the neck) like this: G – G# – A – A# – B – C – C# – D. Continuing in this way, finding the next note around the circle by moving up 7 notes / frets in the chromatic scale, you’ll find all notes in the following order: C – G – D – A – E – B – F#/Gb – C#/Db – G#/Ab – D#/Eb – A#/Bb – F. That is how you find the notes around the circle in the clockwise direction.

You can also find the notes in the anti-clockwise direction by moving along the chromatic scale in Perfect 4th intervals which is a 5 note / fret distance. Again, starting with C you will find the next note to be F like this: C – C# – D – D# – E – F.

Using the above you’ll be able to find out in which order all 12 notes appear around the circle as shown in the diagram at the start of this lesson.

Earlier I mentioned that previous lessons will have given you a good grounding for learning this circle. The guitar strings are tuned (in standard tuning) from the lowest to the highest string in Perfect 4th’s (or a 5 fret distance), the same as the anti-clockwise direction around the circle.

The BEAD-GCF pattern that was easy to remember in the previous lesson can be found by locating the B and then following the circle in the anti-clockwise direction: B – E – A – D – G – C – F – Bb – Eb – Ab – Db – Gb. You can start to see why the guitar is such a great instrument to learn theory on.

Practical Applications

There are many ways in which this circle can help your understanding of music theory and your guitar playing. In this lesson I’ll show one of the things you can do with the circle; how to determine which chords fit in a particular Major key. This will help you when writing your own songs, figuring out songs by ear or when transposing a song to a different key.

Choose a key for which you want to know the chords, for example the key of C. The 7 chords for each key appear in the same order as shown by the Roman numerals. I, ii, iii, IV, V, vi, viiº. Capital numerals denote Major chords while small numerals are minor chords. The viiº is a diminished chord (For a lesson on how to play these chords see: Major, Minor and Diminished Chords).

The chords for the key of C in the example below are (I) C Major, (ii) D minor, (iii) E minor, (IV) F Major, (V) G Major, (vi) A minor, (viiº) B Diminished.

Circle Of 4ths and 5ths

The pattern is always the same as you can see for the key of E Major in the diagram below. Just slide the pattern around the circle until the I is over your chosen key and you’ll know all the chords for that particular Major key.

Now when you hear people talk about a I – IV – V progression in the key of B Major you’ll know what they’re talking about.

If you have a song that uses the progression F# Major – B Major – C# Major but you want to change it to the key of E Major, you do the following. First identify the chord pattern, in this case I – IV – V by having the Roman numeral patterns centered around F#. Then slide the Roman numerals pattern around the neck until the I is over the E. Now you’ll see that the same song in the key of E uses the chord progression E Major – A Major – B Major.

Circle Of 4ths and 5ths

Knowing this will help your song writing as well. Choose a key and then some chords in that key to guarantee good sounding progressions. Experiment with different progressions to see what works and write down the Roman numerals for future reference. Another exercise to do is to figure out the patterns of popular songs, you’ll find that many songs share the same progressions but in different keys. This will help you when figuring out songs by ear.

There are many more things you can do with the circle of 4ths and 5ths and I’ll cover them in future lessons. If you want to learn more about how the Circle of 4ths and 5ths and the Roman numeral system can improve your ability to learn songs and help you write your own music then sign up for the GTR Newsletter.

Lesson 6: The Five Fret Pattern

Derek Trucks
Remember you can zoom in and out on the images in this post by pressing Ctrl + and –

I consider the pattern taught in this lesson to be one of the most important things you can learn in order to help your guitar playing. Once you understand this simple pattern your understanding of how the fretboard works will take a giant leap forwards.

One of the things guitar players struggle with when learning music theory is the confusing way in which numbers are used to describe different musical concepts. For example you may have seen how music intervals (the distance between two notes) are described with terms such as Major 2nd or Perfect 5th. As a guitar player it is confusing to relate these terms to the fretboard because they don’t describe the distance in fret numbers, something which you can easily count.

On top of that you might hear people use terms such as whole and half steps or whole and half tones. This is just another needless level of complexity that doesn’t provide any helpful insights. (In case you are wondering half tones and half steps are a distance of one fret and whole tones and whole steps are two frets distance).

In order to make things much easier to learn and help you understand the inner workings of the fretboard we are going to simplify things. By describing music intervals simply by counting the distance in frets between two notes you easily start to notice patterns that will help you learn chords and scales much quickly and you’ll be able to play them all over the neck with ease.

I call the pattern in this lesson the Five Fret Pattern. The pattern is found by placing your finger on any note on the fretboard, in this first example we’ll pick G# on the low E string. This will be our root note or zero point. Since we’re counting a distance we’ll count this as 0 (in the same way that the start of a ruler is 0 cm or inches).

Five Fret Pattern 1st String

So starting with your finger on the 0 in the white circle, count 5 frets along the string until you reach C#. Now you can also find C# on the 2nd string (the A string) where you see the number 5 in the white circle. The next string up, the number 10 in the white circle is the equivalent of moving 10 frets along the 1st string from the G# on the 1st string. So you can see how all the numbers in this diagram show fret distances from the starting point. Note how the number 24 in the diagram shows a C# but two octaves higher. (You get the next octave up every 12 frets. E.g. 12, 24, 36 etc).

As you can see moving up a string is the same as moving 5 frets along the string. This pattern is easy to remember because its easy to mentally count in groups of 5. The only thing you have to be mindful of is that because of the way the strings are tuned in standard tuning that the pattern on the highest two strings is shifted over towards the bridge by 1 fret.
In the below diagrams you can see what the pattern looks like when you choose your starting point on one of the other strings. Remember that this pattern appears the same way anywhere along the fretboard. All it does is show you relative fret distances.

Five Fret Pattern 2nd String

Five Fret Pattern 3rd String

Five Fret Pattern 4th String

Five Fret Pattern 5th String

Five Fret Pattern 6th String

How knowing the Five Fret Pattern can help you play chords and scales all over the fretboard

Now I’ll show you how this can help your guitar playing. If you know for example that the formula for a Major chord is 0, 4, 7 (0 is the root note plus a note 4 frets along and a note 7 frets along) then you can play Major chords all over the neck by simply placing your fingers on a 0, 4 and 7. (Or equivalents an octave higher. 0+12 = 12, 4+12 = 16 and 7+12 = 19).

Put your finger on a random place on the fretboard and see if you can visualise the Five Fret Pattern with the help of the diagrams. Now see if you can find a 4 and 7 or a 12, 16 and 19 that you can fret at once. Strum these notes and you will have played a Major Chord.

Now see if you can find chords using the Minor Chord formula 0, 3, 7 (Or on higher octaves 0+12 = 12, 3+12 = 15 and 7+12 = 19).

You can also use it to play scales all over the neck. Here is the formula for the Major Scale: 0 – 2 – 4 – 5 – 7 – 9 – 11 – 12. Choose a starting point and count the frets along the string (or on other strings using the diagrams) to find the notes in the scale. 0 is the root note, the next note is 2 frets along, the next one is 4 frets along etc.

Learning this pattern in conjunction with all the names of the notes on the guitar fretboard is one of the best things you can do for your musical education.