Remember you can zoom in and out on the images in this post by pressing Ctrl + and –
Relative scales are scales that share the same set of notes but have different root notes (because they are in different keys). They sound different because their intervals (distance of the scale notes from the root note) are different.
For example here is the C Major scale.
Note Names: C, D, E, F, G, A, B, C
Formula: 0, 2, 4, 5, 7, 9, 11, 12

It sounds the way it does because of the order in which you play the various intervals, from the C to the D (0 – 2), from the D to the E (2 – 4) etc.
But what if you kept the same notes but started on the A in stead? Well then you would be playing the relative (Natural) minor scale of this C Major Scale.
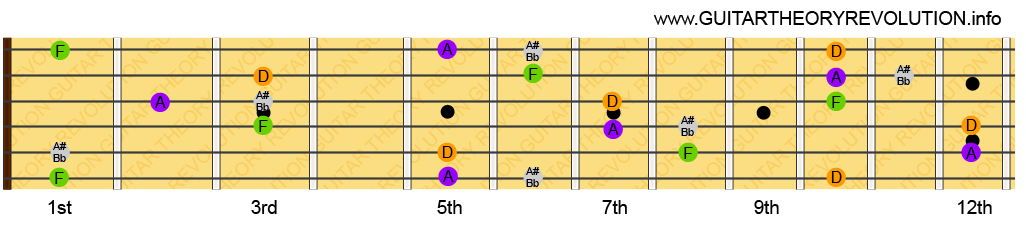
Note Names: A, B, C, D, E, F, G, A
Formula: 0, 2, 3, 5, 7, 8, 10, 12
Using the Five Fret Pattern you can see that although the notes are the same the intervals are different. A to B (0 – 2), B to C (2 – 3) etc.
So to find the relative minor scale of any given Major scale you simply start playing the same notes from the 6th note of the Major scale. To find the relative Major scale for any given Natural minor scale you start at its 3rd note.

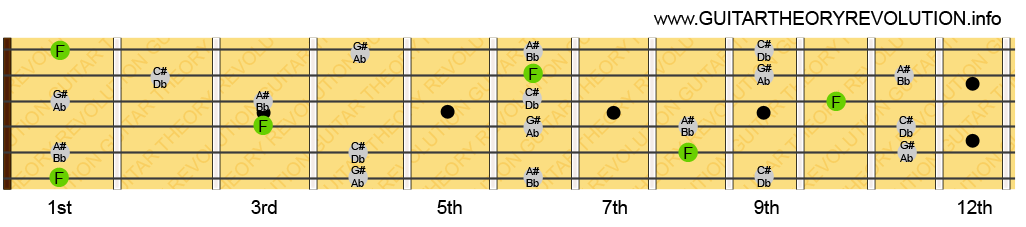
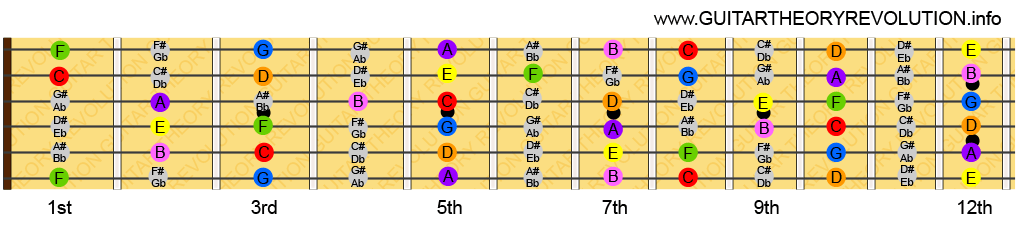
In the above diagram you can see all the notes of the C Major / A Natural minor scale.
Can you see where I got the earlier diagram for the C Major scale from? It starts at the eight fret. So if you want an easy way to find the relative minor scale simply start playing from wherever you see an A. Like the example below.

Knowing how to find the relative minor scale for every Major scale is useful for several reasons. First of all it means that if you know how to play the Major scale you automatically know the Natural minor scale as well.If you practice the Major scale in all 12 keys you’ll know its relative minor in all 12 keys as well.
It means that when you are improvising you can easily switch between the two scales to get a different sound.
Listen to this song Otherside by the Red Hot Chili Peppers (the chord progression for most of the song is Am – F – C – G) and play the above C Major scale over it.
Next play the A minor scale. Can you hear how they sound different?
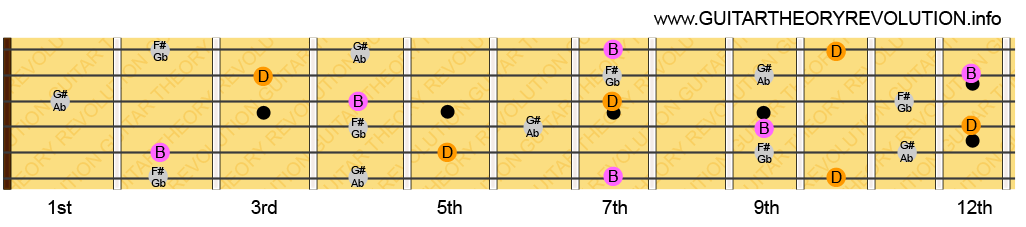
Now use the below diagram to improvise over the music, but rather than sticking to just one scale pattern for each scale, try to play all over the fretboard in stead.
In order to still get the two different sounds choose to switch your focus every 60 seconds or so between the A and C note. So start and end your licks on A for 60 seconds, then start and end your licks on C for the next minute.
For extra bonus points focus on the intervals that are different for each scale: 0-3, 0-8 and 0-10 for the minor scale and 0-4, 0-9 and 0-11 for the Major scale.